Relativity, the relativistic harmonic oscillator, and klystrons
The relativistically amplified musician: This musician's performance is being recorded and transmitted in order to reach a broader audience. The music is captured by a microphone, amplified by a klystron and transmitted through a microwave antenna. Although the klystron is shown schematically here, another schematic below shows the inner workings in more detail.
As a small liberal arts college, Wofford specializes in preparing well-rounded students who have a breadth of experience across all academic fields and a wealth of understanding in the student's major. These requirements, when translated to the physics major, include two semesters of senior research guided by a professor. When it came to my senior year, I wanted to dive deeper into the theoretical underpinnings of mechanics and relativity, so I set my sights for digesting Einstein's field equations. My professor, Dr. Daniel Welch, directed me to spend the first semester studying special relativity through a case study of the relativistic harmonic oscillator and the second semester studying general relativity.
The motivating question of relativity is: "How do two observers subject to a different set of circumstances agree on the measurements that they make?" For special relativity, the difference in circumstances are differences in velocity. By insisting that causal event proceed successively in all inertial reference frames, one can show many surprising result including the facts that an object with momentum will undergo length contraction, time dilation, and mass dilation. For general relativity, the difference in circumstances pertain to non-inertial reference frames, which through Einstein's equivalence principle, are connected to gravitation effects. Despite the unintuitive results, Einstein's theories have held up to experimental scrutiny and have been the original unification theory that combined electric and magnetic effects in a formalism that is consistent with gravity in general relativity.
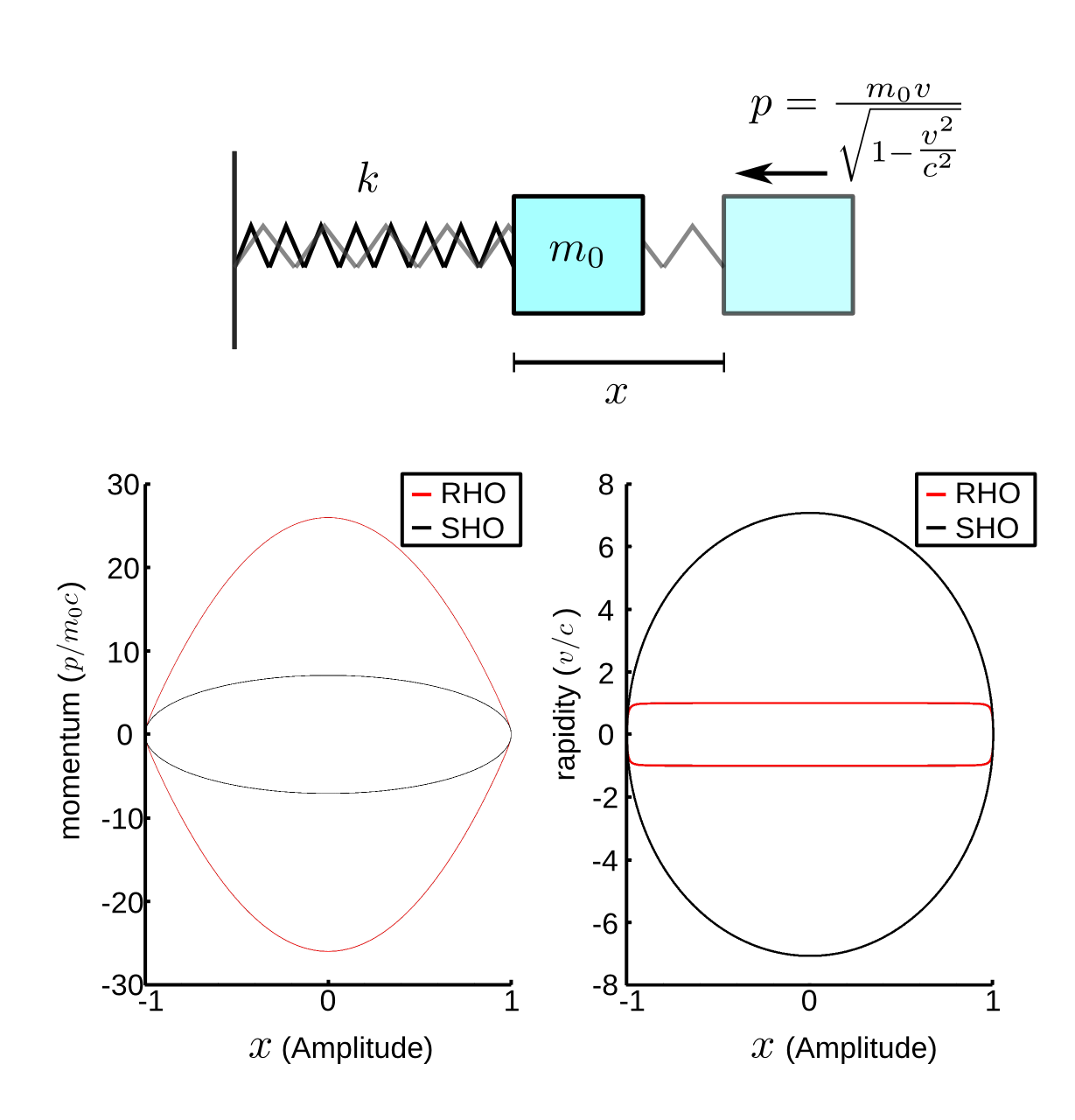
The simple harmonic oscillator serves as a touchstone for many problems that involve bounded repetitive motion partly because the simple quadratic potential has an analytic solution and partly because more complex potentials that result in bounded repetitive motion have the quadratic potential as the lowest order term in its polynomial expansion. As shown in figure 1, the simple harmonic oscillator consists of a mass connected to a spring which in turn is connected to a fixed location. The spring applies a force on the mass, directing the mass to return to a point in the middle of the oscillation, the equilibrium point ($$x = 0$$). The force applied by the spring changes the momentum of the mass, which results in the mass having a maximal momentum when it returns to the equilibrium point. The momentum then carries the mass though the equilibrium point to the other side of the oscillation. When viewed in phase space (a plot of momentum/velocity vs position), the simple harmonic oscillator makes elliptical trajectories.
The relativistic harmonic oscillator takes the quadratic potential from the simple harmonic oscillator and extends the analysis to the high velocity limit (e.g. it is not until $$0.87 c$$ that the Lorentz factor doubles). In this limit, the mass can have an arbitrarily large momentum, but the velocity of the mass is limited to be below $$c$$. As a result, the trajectory of the relativistic harmonic oscillator differs from the simple harmonic oscillator not only in the regions of phase space at high momentum but also in the period of oscillation.
In addition to formulating the equations of motion with Newtonian mechanics as well as with the relativistic Lagrangian and Hamiltonian formalisms, I developed a variation of the Runge-Kutta method for numerically integrating the non-linear equations of motion. I also consulted the literature to verify that my analysis was consistent with previous findings.
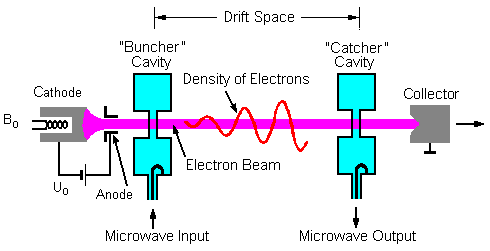
Klystrons (shown schematically in figure 2) take an otherwise uniform-density high-energy electron beam and induce an instability that bunches the electron density. This bunching process mimics the simple / relativistic harmonic oscillator in that the electrons are subject to a force that changes sinusoidally in time while the particle travels across the cavity. As a result, the trajectories of the individual electrons subject to the oscillating electric field are similar to those depicted in figure 1. If the electron beam is initially non-relativistic, then the oscillating electric field will have a significant effect on the velocity change of the individual electrons; however if the beam is relativistic, then the velocity change will be much smaller. The amount of velocity change affects the rate that the electron bunch happens and therefore the necessary length of the klystron tube needed to achieve optimal signal output.
During the second semester of research, I wanted to understand general relativity, in particular the concepts associated with curved space-time and how it related to gravitation. Most of my work was in studying tensor algebra, differential geometry, tangent and cotangent space, the Levi-Cevita connection, and the curvature tensors; however, at the end of the semester, I was able to digest the Newtonian approximation of Einsteinian gravity as well as the Schwarzschild metric. In hindsight, this research experience was useful for my work with surfactants (see the appendix to my dissertation) since a curved four-dimensional space-time requires the same mathematics as a dynamic curved two-dimensional surfactant-covered fluid surface: differential geometry.
A harmonic oscillator (top) consists of a massive object with mass $$m_0$$ connected to a fixed point via a spring with a spring constant of $$k$$. The bottom two graphs show the phase space plots of both the simple (SHO) and relativistic (RHO) harmonic oscillators. Qualitatively, these plots show that when the mass is at the equilibrium point, it experiences no force; however, when the mass is away from the equilibrium, the spring pushes on the mass, changing its momentum, so that the mass eventually returns to the equilibrium point with a maximal momentum. These plots are made for a particle that would be highly relativistic.
A klystron (shown schematically above) amplifies RF and microwave electromagnetic signals. An otherwise high-energy uniform electron beam (generated and focused using the leftmost cathode and anode) is directed down the length of the klystron tube. The input electromagnetic signal accelerates/decelerates electrons in the "buncher cavity" so that over the course of the rest of the beam flight, the electrons bunch, making regions of high density and regions of low density. The acceleration/deceleration of the electrons in the "buncher cavity" mimic the simple (or relativistic) harmonic oscillator. Near the end of the tube, the bunched electron beam passes through a "catcher cavity" giving off a signal much stronger than the input. The remaining energy in the beam is collected and dissipated as heat. Most klystrons also have focusing/rectification cavities to ensure that the high energy output signal has the correct wave form.
