Strickly Research

Research - Surfactant

Two-dimensional materials, pulmonary surfactant replacement therapy, and mock oil spills

The meticulous varnisher: A violin maker applies surfactant based varnish to a violin while a second instrument hangs to let the varnish dry. Varnish serves the two fold task of encasing and protecting the wood and enhancing the visual qualities of the wood. The varnish coating also affects the accoustics of the wood; however, because of the wide range of varnish preparation methods, the precise effects and best methods are debated among luthiers. Many varnishes, as with many paints and inks, contain fatty acids (a class of surfactants). These surfactants contribute to the coating's chemical and mechanical properties as well as the structure of the varnish.

How do surfactants spread?

The video above shows NBD-PC (a surfactant) spreading on a 0.7 mm deep film of glycerin. The surfactant concentration is measurable through the fluorescent emission of the surfactant layer, while the motion of the glycerin film is measurable through the motion of the laser line projected obliquely at the glycerin surface.

The surfactant is initially contained within a ring in the center of the stage. Once the ring separates from the surface (and is manually removed from the field of view), the surfactant appears as a brighter circular patch in the center that spreads outwards. The bright horizontal line is from a laser line generator. When the surface is flat, the line is flat. When the surface is curved, the laser line also curves. The variations in the laser line are proportional to the variations in the depth of the glycerin film. The localized bright spots outside of the surfactant patch are due either to reflections from imperfections in the silicon wafer beneath the glycerin or dust.

Of particular import is the motion of the Marangoni ridge (the fluid ridge that travels outward) and the leading edge of the surfactant. The two are roughly coincident, and for high surfactant concentrations (as shown above), the leaning edge travels as r~t^1/4

How do surfactant layers heal?

This video shows NBD-PC (a surfactant) self-healing on a 0.7 mm deep film of glycerin. In this geometry, the surfactant is deposited outside of the ring while the region within the ring is left clean. This system represents a situation where an otherwise homogeneous surface coating has been damaged. The visualization methods for the surfactant concentration and glycerin dynamics are the same as in the first video.

As the surfactant spread inward, the Marangoni ridge coalesces into a central distension. This distension then slowly relaxes back to a flat surface.

Where is the surfactant on a wave?

This video shows the motion of NBD-PC, a surfactant, as moved by gravity-capillary waves on the surface of a 7 mm deep layer of water. The gravity-capillary waves consist of a super position of standing Faraday waves and traveling meniscus waves. The surfactant accumulates in the troughs of the standing waves and on the leading edge of the traveling waves. This video was produced for the 2014 DFD conference and produced with Final Cut Pro X.

What are surfactants?

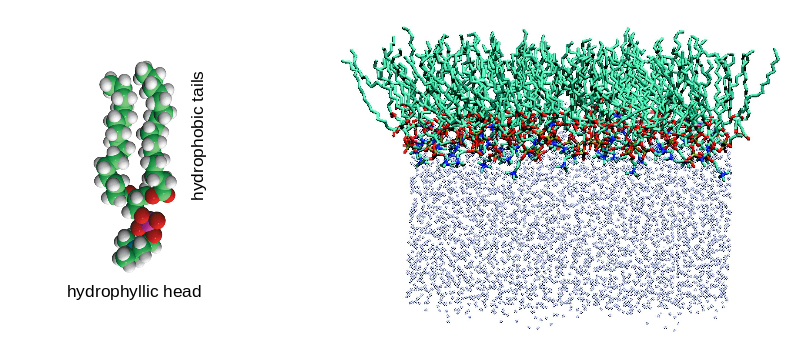
Surfactants are a class of materials, for example soaps or detergents or fatty acids, that have a two-part molecular structure where one part is attracted to water and the other part is not. As a result, these materials form thin layers at the surface of water which can reduce the surface tension of water. Consider the zwitterionic molecule DPPC (left image). The polar head group is attracted to the polar water molecules while the two non-polar hydrocarbon tails are entropically repelled by water molecules. At the surface of water, DPPC forms a layer that is a single molecule thick (right image) and acts like a two dimensional material.

Why do surfactants matter?

Surfactants matter because of the many applications that involve stabilizing surfaces, for example:

pulmonary surfactant replacement therapy
soaps, detergents, and degreasers
emulsions and food stabilizers
non-stick and self-cleaning coatings
fire fighting foams
inks and paints

These applications use different surfactant materials, and the choice of material is based upon the physico-chemical properties. On the macroscopic scale, the primary mechanical properties include the equation of state (the surface tension vs surfactant concentration relation), the surface dilational, shear, and bending modulus and viscosities, the critical micelle concentration (for soluble surfactants), and the rheological effects of the surfactant on the bulk of the subphase (e.g. wormlike micelles).

Motivation for our research

We know that surfactants have a significant impact on their liquid subphases ^{[
1,
1,
1,
1,
1
]}; however, there has not been a method for measuring the distribution of the surfactant layer for dynamic processes, at least not on a macroscopic scale.

For example, consider the remote detection of oil spills. The oil damps ocean waves via its ability to reduce surface tension. Satellites are able to tell if the oil spill has entered a given region by measuring the smoothness of the ocean surface (via the intensity of radar as reflected off the ocean surface); however, these images do not report the density of the oil (how it is distributed).

As another example, consider the first demonstration in this classic NSF fluid mechanics video (time 0:31-1:03) where the presenter stretches a thin soapy film. Although the effects of the surfactant are evident in the stabilization of the film, the dynamics of the surfactant layer are unknown.

Measuring the distribution of the surfactant provides more information, not only about where the oil is for its clean up but also about the dynamic coupling between the surfactant layer and the sub-phase. The precise nature of the coupling is still unknown. Things like the boundary condition (whether or not there should be a slip length at the surfactant-covered surface), mechanical properties about the surfactant layer (e.g. shear and dilational elasticities and viscosities), or the mechanical response/driving of the surfactant layer in a variety of situations. These are, to various degrees, unknowns partly because of a lack of a method to measure the surfactant distribution.

What have we contributed?

In Karen Daniel's research group, I have contributed an optimized experimental technique which permits measurements of the surfactant distribution over a macroscopic region of the surface. The technique is non-invasive as it relies on a fluorescent emission from a designer surfactant, and it has a temporal resolution on the order of a tenth of a second. We have used this technique to study three situations in two physical systems:

Surfactant spreading on a thin fluid film (published)
Surfactant self-healing on a thin fluid film (published)
Surfactant motion on gravity-capillary waves (published)

The surfactant spreading and self-healing experiment are interesting both because of the likeness to processes involved in pulmonary surfactant replacement therapy but also because the sub-phase in surfactant spreading systems exhibit a wide range of fingering and spreading behaviors ^[1,1,1]. For the case of a surfactant (initially localized to a circular area) spreading outward (How do surfactants spread?), we found that the spreading of a monolayer of surfactant differs from the spreading of a more dense (multi ?)-layer, and that in some cases, the spreading can stall. For the related case of a surfactant (initially in an annular configuration) spreading inward (How do surfactant layers heal?), we again observed the spreading of high initial concentrations and the stalling of low, and we also observed the formation and decay of a distension in the center of the annulus. These studies highlight the fact that surfactant layers do not always coat the sub-phase and that the specific equation of state needs to be included in theoretical considerations to account for some of the dynamics. Since surfactants are used to coat materials for industrial applications, this can have significant consequences.

The surfactant dynamics on gravity-capillary waves are of interest in part because it mimics oil spill like situations but also because the waves are a periodic disturbance which can undergo instabilities and non-linear processes. As shown in the video "Where is the surfactant on a wave?", the surfactant accumulates in different places depending on the type of wave. For standing Faraday waves, the surfactant accumulates in the troughs, contrary to the expectations of the linearize theory. For traveling meniscus waves, the surfactant accumulates on the leading edge, an asymmetry which may suggest that waves provide a directed transport of surfactant.